Microsoft Access Regression Calculations with Total Access Statistics
Microsoft Access does not offer regression analysis, but writing your own regression calculations which involves matrix inversions is quite complicated and time consuming.
Fortunately, Total Access Statistics can generate regressions on your Microsoft Access tables and queries. All results are in MS Access tables that you can use on your forms, reports, and VBA code.
Introduction to Regressions
A regression calculates the least squares (best fit) line or curve to determine an equation which relates the Y dependent variable to the X independent variable(s).
Total Access Statistics makes it very easy to calculate the regressions in MS Access:
- Analyze the data from Microsoft Access tables and queries (including linked data)
- An unlimited number of records may be calculated in one pass.
- Optionally specify GROUP BY fields so you can perform regressions for each set of grouped records in one pass
- Optionally specify a weighting field
- Optionally specify a value or range of values to ignore
All the options can be selected interactively through the add-in Wizard interface. VBA developers can run the analysis through a programmatic VBA function call.
Field selection is very simple:
- One numeric field must be designated the Y field
- At least one X field must be assigned
- Group and Weight fields are optional
A separate calculation is made for each group of records (combination of unique Group fields values). A separate record is created for each group and X field.
Regression Field Selection for Cholesterol versus Weight for each State
After you select your fields and press the [Next] button, the Regression options appear.
Choose among three regression types and two calculation options:

Total Access Statistics supports the generation of Simple, Multiple, and Polynomial regressions:
Simple Linear Regression
A linear (simple) regression is calculated between the Y field and each X field using this simple equation:
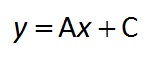
where A and C are the constants that are solved. “A” is the slope of the line, “C” is the y-intercept. One equation (record) is created for each set of group fields and X field.
Multiple Regression
A multiple regression of the linear combination of X fields to the Y field is calculated. All X fields are assumed to be independent variables. At least two X fields must be assigned; otherwise you should use simple regression. Here's the multiple regression equation:
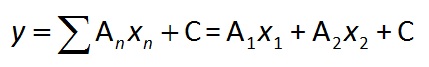
where xi is the ith X field, and Ai and C are constants. Any record with a blank X field or Y field is ignored. One equation (record) is created for each group of check fields.
Polynomial Regression
A polynomial regression between each X field and Y field is calculated based on this equation:
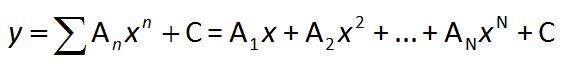
where N is the polynomial order, and Ai and C are constants. The polynomial order (up to 9) determines the maximum power (exponent) of X in the equation. Any record with a blank X or Y field is ignored. One equation (record) is created for each group of check fields and X field.
Calculate Y-Intercept
This option controls whether the y-intercept (C constant) is calculated or set to zero (through the origin). If this option is checked, the y-intercept is calculated.
Calculate Regression ANOVA
If this option is selected, each regression’s ANOVA values are calculated. The field names are described later.
You can optional choose to create a residual table and assign the estimated Y value to a field in your data source:
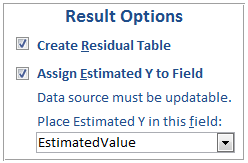
Create Residual Table
If this option is selected, a separate Residual table is created. The residual table contains one record for each data point used in the regression calculation along with residual information. The Residual is the difference between the actual Y and the regression’s estimated Y value.
Assign Estimated Y to Field
The value of Y based on the regression equation can be inserted directly into a field on each record. This feature is available when only one regression equation is being created for each record. This is always the case for a multiple regression. For simple and polynomial regressions, this exists if only one Independent (X) field is selected.
Simply specify the field where you’d like the result to be placed. The field should be a double and the data source must of course be updateable.
The following examples are different types of regressions for comparing X fields [Age] and [Weight] against Y Field [Cholesterol], grouped by [State] (not all fields shown).
Simple Regression

Multiple Regression

Polynomial Regression (Order 3)

Regardless of which options are selected, the output table for Regression always includes these fields:
| Field Name | Description |
|---|---|
| Group Fields | Group fields selected (if any) |
| DataField | Field name identifying the data in the record |
| Count of Y Field | Number of records in the group, where Y Field is the name of the Y Field |
| Missing | Records with missing values |
| Multiple R | Square root of R-Square |
| R-Square | R-Square measures the proportion of variation in Y that is explained by the regression. R-Square is between 0 and 1 (1 is a perfect fit). |
| Adj_R-Square | Adjusted R-Square |
| StdError_of_Estimate | Standard error of the Y estimate (regression) is the standard deviation of the residuals |
| Y-Intercept | Y-Intercept value, if this option is selected |
| Coef_of_X | Coefficient(s) of the regression equation |
The regression coefficient fields vary depending on the type of regression selected:
- Simple Regressions: one field for the X coefficient.
- Multiple Regression: one field for each X field: Coef_of_X1, Coef_of_X2, Coef_of_X3, etc.
- Polynomial Regressions: one field for each polynomial order: Coef_of_X^1, Coef_of_X^2, Coef_of_X^3, etc.
In addition to the Y-Intercept and equation coefficients, four other fields are calculated for each coefficient to determine the accuracy and relative importance of each coefficient. The four fields are explained below with the field names in brackets:
Standard Error of Coefficients [SE_of_X]
Standard Error of Coefficients is a measure of each coefficient’s variability. Although the coefficient is calculated, the sample data is assumed to contain variability. The population coefficient is the sample coefficient plus or minus the standard error.
Beta Value of Coefficients [Beta_of_X]
Beta Value of Coefficients (also known as standardized regression coefficients) shows the relative importance of each coefficient in the regression equation. For multiple and polynomial regressions, it can be misleading to examine only the unstandardized coefficients for importance. A large coefficient may have little impact if its variable does not vary much. The Beta removes this effect. Beta is not calculated for the Y-Intercept.
t-Value of Coefficients [t-Value_of_X]
The t-Value of the coefficient is used to determine (via t-Test) the probability that the coefficient value is significantly different from zero. t-Value is the ratio of the Coefficient to its Standard Error.
Probability of Coefficients [Prob_of_X]
Probability of coefficients determines the probability that the coefficient is zero based on its t Value.
The regression ANOVA indicates how much of the data variance is due to the regression, and how much is not (residual). If the regression has a poor “fit” (large residual), the F-Value is small and the probability that all regression coefficients are zero (the null hypothesis) approaches 1. These are the ANOVA fields:
| Field Name | Symbol | Description |
|---|---|---|
| Regression_DF | DF | Regression degrees of freedom. Number of independent variables. |
| Residual_DF | DF2 | Residual degrees of freedom = N - DF1 - 1 (where N is the number of data points) |
| Total_DF | DFT | Total degrees of freedom = N – 1 |
| Regression_SS | SS1 | Regression (estimated-average) sum of squares |
| Residual_SS | SS2 | Residual (actual-estimated) sum of squares |
| Total_SS | SST | Total sum of squares = SS1 + SS2 |
| Regression_MS | MS1 | Regression mean squares = SS1 / DF1 |
| Residual_MS | MS2 | Residual mean squares = SS2 / DF2 |
| F-Value | F | Ratio of mean squares = MS1 / MS2 |
| Prob | P | Probability (0-1) that all coefficients = 0 |
If the Residual table option is selected, a second table is created:

This table contains all data (X and Y) used in the regression as well as the estimated Y value and the residual. A record is created for every data point. Data that is not used in the regression (blank values) or groups for which a regression could not be calculated are not included in the Residual table.
| Field Name | Description |
|---|---|
| Group Fields | Group fields selected (if any) |
| DataField | Field name identifying the data in the record |
| X Value | Value of the X Field |
| Y Field | Actual Y value from the data source |
| Estimated Y | Estimated Y value based on the regression equation and the calculated coefficients |
| Residual | Difference between the actual and estimated Y values |
From the residual table, you can create a graph that plots the individual data points and a line through the estimated Y values to see the regression equation.
Total Access Statistics lets you interactively generate your calculations through its wizard interface to easily select the data source, fields, and analysis without programming. After you specify your selections, they are automatically saved as a scenario in your database so you can run them again in the future when your data changes.
A VBA statistics function is also available so you can generate these results from code. You can easily run any saved scenario by calling a single procedure in the Total Access Statistics VBA library. The library includes a royalty-free runtime license so you can include it with your Access database and distribute it to non-Total Access Statistics owners.
Call the function from a button's OnClick event or other process, and the results are generated for you. You can even hide the built-in user interface so your users don't even know Total Access Statistics is running. They'll be amazed with your statistical analysis capabilities!
Here are some additional resources and details about some of the data analysis you can perform on your Microsoft Access data with Total Access Statistics:
-
 Financial Cash Flow Calculations
Financial Cash Flow Calculations
Use discounted cash flows and interest rates to generate Net Present Value (NPV), Present Value (PV), Future Value (FV), Internal Rate of Return (IRR), Modified Internal Rate of Return (MIRR) for periodic and date dependent payments and receipts. -
 Percentile Calculations
Percentile Calculations
Calculate different types of percentiles: median, quartiles, quintiles, octiles, deciles, percentiles, every X.5 percentile, and place them in a table or update an existing field with the record's percentile value. - Running Totals and Moving Averages
Summarize a moving set of records to calculate running sums, moving averages, minimum, maximum, range, median, standard deviation, etc. - Data Normalization (Data Transpose)
Transpose non-normalized data so you can easily analyze and maintain it. - Regressions
Simple, multiple and polynomial regressions with calculation of equation coefficients, ANOVA and residual table - Crosstabs and Chi-Square
Advanced cross-tabulations with percentage of row, column and totals displayed as records or columns
Microsoft Access 2016 and 2013 Versions are shipping!
Version 14.1 for
Microsoft Access 2010
Version X.9 for
Microsoft Access 2007 and 2003
Version X.8 for
Microsoft Access 2002, 2000, and 97
Reviews
"Total Access Statistics performs a wide range of data analysis right inside Access. The product includes a Statistics Wizard to perform parametric, group, non-parametric, record analysis and more. The results are placed in Access tables that you can integrate into your forms and reports."
Alison Balter, Author
Statistics Info
Additional Info